I/D #1: Unit N Concept 7: How do Special Right Triangles and the Unit Circle relate?

INQUIRY ACTIVITY SUMMARY

Before moving onto the next concept, we were given this chart to figure out on our own (with the help of Google) how to label the special right triangles. The first thing I did was use Google, of course, and found the following images below. For the activity we had to simplify the sides so that the hypotenuses would equal to 1. Next was labeling the sides with variables. The hypotenuse (the longest side- opposite of the 90°) is labeled by "r", the horizontal value by "x", and the vertical value by "y". After doing this, we had to draw a coordinate plane for each triangle making it so that the triangle lies in Quadrant I. Our final step was labeling all three vertices of each triangle as ordered pairs.

(http://www.montereyinstitute.org/courses/DevelopmentalMath/COURSE_TEXT2_RESOURCE/U19_L1_T3_text_final_3_files/image022.gif)

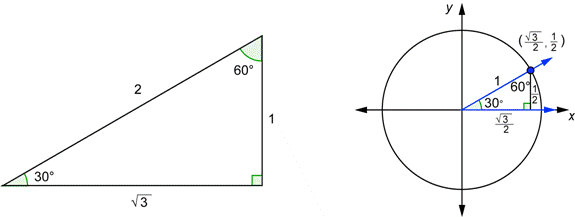
1. Describe the 30° 

In a 30° SPT triangle, we know that all three angles will equal to 180°. Since 30° is given and we know that it's a right angle (90°), then we know that the last angle will be 60°. We focus on the 30° angle and we label accordingly. The opposite side from the 30° is x/2x. The side adjacent is x√3. The hypotenuse is always across from the 90° angle and it is 2x. 
To get the hypotenuse to equal to 1, we have to divide all the sides by 2x. By doing so, the hypotenuse will be the desired value of 1, the x-value we will have x√3/2x which when you cancel out the x's, will be √3/2. For our y-value (vertical value), we divide 2x from x and we will end up with 1/2. 
          To find the ordered pairs, we just find the points plotted on the circle. The UC revolves around it's center point (0,0) which is one of the vertices. On a graph, we use (x,y) for our points and now we can just apply the same concept. Since the x-value is √3,2 and our y-value is 1/2, our first vertices at the top corner will be (√3/2, 1/2). Our last point is where the 90° angle is. Since it lies on the x-axis only, we know there won't be a y-value so our ordered pair is (√3/2, 0). 

          

(http://www.montereyinstitute.org/courses/DevelopmentalMath/COURSE_TEXT2_RESOURCE/U19_L1_T3_text_final_3_files/image035.gif)
(http://www.montereyinstitute.org/courses/DevelopmentalMath/COURSE_TEXT2_RESOURCE/U19_L1_T3_text_final_3_files/image036.gif)

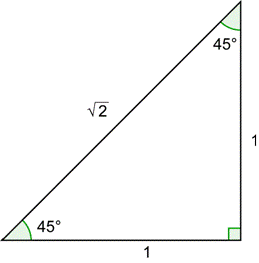
2. Decribe the 45°

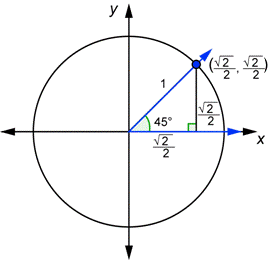
In a 45° SPT trianlgle, we know that the two angles will be 45° because they add up to 90° and our right angle will make up the total of 180°. Since the length of the two sides are equal, they're both labeled "x" on the horizontal and vertical axis. The hypotenuse is x√2. 
          Since we are working with a unit circle, we want our radius (ultimately our hypotenuse) to be 1. To do this, we have to divide x√2 to all sides. So our hypotenuse will end up with 1, just how we wanted. When we divide x√2 from x, the x's will cancel out and we will be left with 1/√2 and since radicals aren't allowed to be in the denominator of a fraction, we have to mulitply it by √2 on the top and bottom so our answer will be √2/√4, but the √4 will be square rooted to 2. Our x-value (horizontal value) will be end up to be √2/2 and our y value (vertical value) will also be 2√2.
         We know that our origin will always be at (0,0) and that is our first vertices. Since we know our x and y-value are both √2/2, our ordred pair will be (√2/2, √2/2). Our third vertices will lie on the x-axis and it will end up to be (√2/2, 0)
      

(http://www.sparknotes.com/testprep/books/sat2/math2c/chapter6section2.rhtml)

(http://www.montereyinstitute.org/courses/DevelopmentalMath/COURSE_TEXT2_RESOURCE/U19_L1_T3_text_final_3_files/image108.gif)

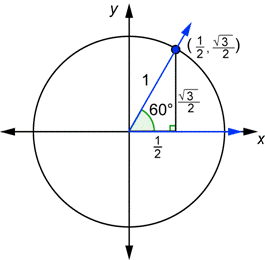
3. Describe the 60°

In the 60° angle SRT, it's exactly the same as the 30° angle one but the value of the sides are switched around. The hypotenuse stays the same with 2x, however the horizonatal and vertical value switch. So for the x-value, it is now just x, while the y-value is x√3. To get the hypotenuse to equal one, we do the same thing as before and divide everything by 2x. We end up with the x-value to be 1/2 and the y-value as √3/2. 

          Just like the other triangles, we have a point at our origin, (0,0). Our x-value is 1/2 and our y-value is √3/2 so our point will be (1/2, √3/2). The third point is on the x-axis as well and it is (1/2, 0).

4. By doing this activity, we derive how to find the ordered pairs in a unit circle. We also notice that the triangles are in the circle so it's easy to understand where we got the numbers from instead of just memorizing and not having the background knowlege of where the numbers came from. We can easily find out the value of the sides for the ordered pairs by just referring back to the special right triangles. It helps us build a better understanding of the circle. 

5. In the activity, we focused our trianlges to be in the first quadrant so it could easily be understood. The values start to change when we move it into different quadrants.

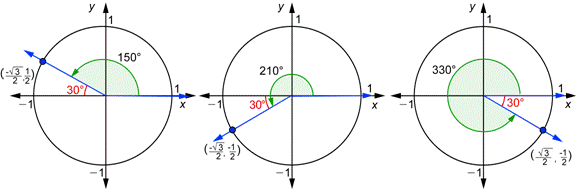
(http://www.montereyinstitute.org/courses/DevelopmentalMath/COURSE_TEXT2_RESOURCE/U19_L1_T3_text_final_3_files/image100.gif)

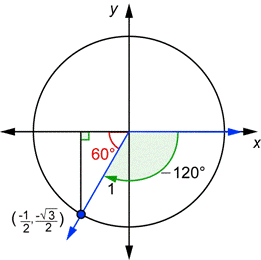
In the picture above, it shows a 30° angle in the II, III, and IV quadrant. The only thing that changes is the negative signs. In the second quadrant, the x-value bececomes a negative and that's the only thing that changes. However, in Quadrant III, both of the values are negative. In the fourth quadrant, only the y-value of the ordered pair is quadrant.

The pictures on the right show a 45° angle in the II, III, and IV. The only thing that changes in the second quadrant is the negative sign on the x-value. In the thirf quadrant, both numbers are negative, while in the last one, only the y-value is negative.

(http://www.montereyinstitute.org/courses/DevelopmentalMath/COURSE_TEXT2_RESOURCE/U19_L1_T3_text_final_3_files/image036.gif) ^original picture but I editted it into the other three quadrants.

(http://www.montereyinstitute.org/courses/DevelopmentalMath/COURSE_TEXT2_RESOURCE/U19_L1_T3_text_final_3_files/image118.gif)

(http://www.montereyinstitute.org/courses/DevelopmentalMath/COURSE_TEXT2_RESOURCE/U19_L1_T3_text_final_3_files/image111.gif)

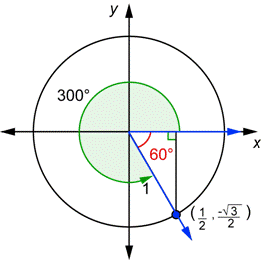
Just as the other pictures, in the above picture is an example of the 60° SRT in the 3rd and 4th quadrant. In an example of the triangle in the 2nd quadrant (not shown), the x value would be negative. In the third quadrant, both x and y-values are negative. In Quadrant 4, only the y-value is negative.

INQUIRY ACTIVITY REFLECTION

1. The coolest thing I learned from this activity was how the SRT and UC connected together and were in a way dependent on each other for our learning.
2. This activity will help me in this unit because it helped me better understand how to find the values of the sides which ultimately gave me the ordered pairs of the circle. Instead of memorizing numbers, by connecting the two, it helped me understand and showed me how I can easily find the value if I forgot the memorization parts.
3. Something I never realized before about special right triangles and the unit circle is how it both went together. I never saw the triangles in the circle until we did the activity before entering Concept 7.

WORKS CITED

1.http://www.montereyinstitute.org/courses/DevelopmentalMath/COURSE_TEXT2_RESOURCE/U19_L1_T3_text_final_3_files/image022.gif
2. http://www.montereyinstitute.org/courses/DevelopmentalMath/COURSE_TEXT2_RESOURCE/U19_L1_T3_text_final_3_files/image035.gif

3.http://www.montereyinstitute.org/courses/DevelopmentalMath/COURSE_TEXT2_RESOURCE/U19_L1_T3_text_final_3_files/image036.gif

4.http://www.sparknotes.com/testprep/books/sat2/math2c/chapter6section2.rhtml)

5.http://www.montereyinstitute.org/courses/DevelopmentalMath/COURSE_TEXT2_RESOURCE/U19_L1_T3_text_final_3_files/image108.gif
6. http://www.montereyinstitute.org/courses/DevelopmentalMath/COURSE_TEXT2_RESOURCE/U19_L1_T3_text_final_3_files/image100.gif
7. http://www.montereyinstitute.org/courses/DevelopmentalMath/COURSE_TEXT2_RESOURCE/U19_L1_T3_text_final_3_files/image036.gif
8. http://www.montereyinstitute.org/courses/DevelopmentalMath/COURSE_TEXT2_RESOURCE/U19_L1_T3_text_final_3_files/image118.gif
9.http://www.montereyinstitute.org/courses/DevelopmentalMath/COURSE_TEXT2_RESOURCE/U19_L1_T3_text_final_3_files/image111.gif

RWA 1 Unit M Concept 4 - Conic Sections in Real Life

1. Ellipse- 

"The set of all points such that the sum of the distance from two points is a constant." (Kirch)

2. Algebraically, the equation of an ellipse can be either:

(http://www.purplemath.com/modules/ellipse.htm)

or


(http://www.purplemath.com/modules/ellipse.htm)

Graphically, an ellipse will look like a squished circle.

 
when "a" is under y^2
(http://tutorial.math.lamar.edu/Classes/Alg/Ellipses.aspx)

when "a" is under x^2
(http://tutorial.math.lamar.edu/Classes/Alg/Ellipses.aspx)


Depending on the which variable comes first, the ellipse can either be "fat" or "skinny".

          Before graphing the equation of an ellipse, we must find the components to plot. The equation must be in standard form and it must equal to 1. Remember that the h and k in the equation match up with x and y value which will end up being our center point. After we identify the center, we plot it. The major axis (a) is the distance from the vertex to the center and is the longer one. The minor axis (b) is the distance between the co-vertex to the center and it is the shorter one. In a given equation, we can easily determine "a" and "b" by taking it from the denominator and finding the square root of it. The bigger number will be "a" while the smaller one will be "b". 
          To determine whether the major axis is horizontal or vertical, we look at the bigger number under the term. If the bigger number is under the x^2 term ,then the major axis will run horizontally. However, if it's under the y^2 term, the major axis will run vertically. Remember to note that from this information we already figured out, we can determine what the shape will look like. If the bigger number is under the x^2 term, we know that the shape will be fat and if it's under the y^2 term, it will be skinny. (X-tra FAT, Y so SKINNY) To find c, which is the distance between the focus point to the center, we use the formula a^2 - b^2=c^2. So we plug in our known terms, a and b, to find c. To plot the point for our vertices, co-vertices, and foci's we need to use all the information we were given or found. Once we find our whether our shape is fat or skinny, we can also find our major and minor axis which will either be "y=" or "x=". (These values can be found from our center point, if given!)  Using the x and y values, we can put it into the corresponding spots in our vertices and co-vertices. To find the other number, we take the a or b value and find the distance from the center point.  
          For example, if our major axis is "y=3", we know that the line will be horizontal. So for our two vertices point, the y-values will both be 3. To find the x-value of our ordered pair, we use "a" and add it to the x-value of the center point for one of the points, then subtract the same number for the other point. Then, if our minor axis is "x=9",the co-vertices pair will have 9's in the x spots. To find out the other number of the pair, instead of using "a", we use the "b" variable and find the y-values for our co-vertices. As for "c", we keep the major axis point the same, which is 3, but for the x-value, we have to add and subtract it to our "c" variable. When we plot the points on the graph, we need to remember that the foci will be inside the ellipse, it should not go beyond the vertices. 
          The foci affects the shape of the conic because it can help determine whether the conic is skinny or fat. If you're still unsure whether the conic is skinny or fat, plotting the foci can be a tremendous help because we know that the foci will always lie with the major axis. So if your major axis is y, then your foci will also end up on y. We know that if "y=something" the line will be horizontal which signifies that it will be fat. Vice versa, if the major axis is "x=something" the line is vertical and the conic will be skinny. Eccentricity is the measure of the amount of how "squished" an ellipse is from being perfectly round. We find eccentricity be taking c/a. For an ellipse, the eccentricity should be 0<e<1, between 0 and 1. 

For a better understanding of the components of an ellipse and a thorough example, check out this video by PatrickJMT:

3. Real world applications of ellipses 

          Ellipses can be found within our solar system. The sun is a focus point while the orbits in planets are ellipses. Because planets also have focus points, the orbit are elliptical. "The short answer is: it falls out of the math.  Specifically, the math of first year physics and second year calculus.  The fact that the Sun is in one focus is just one of those things.  It’s nothing special.  Even less special is the other focus, which contains nothing at all."(http://www.askamathematician.com/2010/08/q-why-are-orbits-elliptical-why-is-the-sun-in-one-focus-and-whats-in-the-other/)

          The chain wheel on a bike is also an example of an ellipse. Although it is slightly a little off from an elllipse, it has the elliptical shape.  "Here the difference between the major and minor axes of the ellipse is used to account for differences in the speed and force applied, because your legs push and pull more effectively when the pedals are arranged so that one pedal is in front and one is in back, than when the pedals are in the "dead zone" (when one pedal is up and one pedal is down)." (http://answers.yahoo.com/question/index?qid=20061130170749AAlmTyj)

4. References/Works Cited

• http://www.purplemath.com/modules/ellipse.htm
• https://www.youtube.com/watch?v=5nxT6LQhXLM
• http://answers.yahoo.com/question/index?qid=20061130170749AAlmTyj
• http://tutorial.math.lamar.edu/Classes/Alg/Ellipses.aspx
• http://www.askamathematician.com/2010/08/q-why-are-orbits-elliptical-why-is-the-sun-in-one-focus-and-whats-in-the-other/